Cp and Cpk are used for Process Capability. Generally, you use this when a process is under statistical control. This often happens with a mature process that has been around for a while. Process capability uses the process sigma value determined from either the Moving Range, Range, or Sigma control charts.
Pp and PPk are used for Process Performance. Generally, you use this when a process is too new to determine if it is under statistical control.
Ex. you are piloting a new process or testing a short pre-production run. Because there is not a lot of historical data, we take large samples from the process to account for variation. Process Performance generally uses sample sigma in its calculation.
In theory, Cpk will always be greater than or equal to Ppk.
There are anomalies seen when the sample size is small, and the data represents a short amount of time where estimating using R will overstate standard deviation and make Cpk smaller than Ppk. It is not real; there can never be less variation in the long term since the long term is using all of the data, not just two pieces of data from every subgroup.
Cpk vs. Ppk
Ppk tells us how a process has performed in the past, and you cannot use it to predict the future because the process is not in a state of control.
If a process is under statistical control;
The values for Cpk and Ppk will converge to almost the same value because the sigma and the sample standard deviation will be identical (use an F test to determine).
In other words, if Cpk == Ppk, the process is likely in statistical control.
If a process is NOT in statistical control;
Cpk and Ppk values will differ distinctly, perhaps by a very wide margin.
How we calculate Cpk:
Cpk is a measure to show how many standard deviations the specification limits are from the center of the process. On some processes, you can do this visually. Others require an equation.
To find Cpk you need to calculate a Z score for the upper specification limit (called Z USL) and a Z score for the lower specification limit (called Z LSL).
To calculate the Cpl, subtract the lower specification limit from the mean, then divide this by 3 times the standard deviation (SD):
Cp is an abbreviation. There are really two parts, the upper and the lower denoted Cpu and Cpl, respectively. Their equations are:
Cpl = (Process Mean – LSL)/(3*Standard Deviation)
To calculate the Cpu, subtract the upper specification limit from the mean, then divide this by 3 times the standard deviation (SD):
Cpu = (USL – Process Mean)/(3*Standard Deviation)
Cpk is merely the smallest value of the Cpl or Cpu denoted: Cpk= Min (Cpl, Cpu)
Cpk can be determined by dividing the Z score by three.
A z score is the same as a standard score; the number of standard deviations above the mean.
Z= (X-Micro)/Sigma
Z = x – mean of the population / standard deviation.
Z USL = USL – Process Mean / Standard Deviation. then becomes Z USL = A/ Standard Deviation
Z LSL = Process Mean – LSL / Standard Deviation then becomes Z LSL = A / Standard Deviation.
Notes on Cpk
- Cpk measures how close a process is performing compared to its specification limits and accounting for the natural variability of the process.
- Larger is better. The larger Cpk is, the less likely it is that any item will be outside the specification limits.
- When Cpk is negative, it means that a process will produce output that is outside the customer specification limits.
- When the process’s mean is outside the customer specification limits, the value of Cpk will be negative.
- To satisfy most customers, we generally want a Cpk of at least 1.33 [4 sigmas] or higher.
- Cpk can have an upper and lower value reported.
- If the upper value is 2 and the lower is 1, we say it has been shifted to the left.
- This tells us nothing about whether the process is stable or not.
- We must report the lower of the 2 values.
Cpk Formula :
CP stands for Process Capability (Cp), it is a technique to find out the measurable property of a process to a specification. And Cpk stands for Process Capability Index (Cpk). It measures the producer’s capability to produce a product within the customer’s tolerance range. Cpk is used to calculate how close you are to a given target and how consistent you are to your average performance.
Cpk gives you the best-case scenario for the existing process. Let us study the basics of cpk and cpk formulas.
What is Process Capability Index
Process Capability is a calculation tool used by many to estimate the product output. After the industrial revolution that introduced machine lines for production, the method of manufacturing turned into a controlled process. Later the investors tried to make calculations based on the observed speed of factors of production.
They wanted to estimate the possible output they are going to have to calculate and manage the resources for maximum performance.
The inputs for the process capability index are usually the normal statistical analysis and distribution of data obtained. It is somewhat similar to ‘mean’ or ‘average value’ and the ‘standard deviation’ that is taught in arithmetic.
But it differs in the terms of using a control chart analysis to check the statistical control of the data. Usually, three measured output data is used. The data of production conditions, materials and people involved in the process is taken into consideration.
This method is utilized by both established production units and startups. The outputs are obtained in the plus and minus deviations. The Whole process is responsible.
for understanding and meeting customer requirements, engineering tolerance and specifications of manufacture of produced goods.
When this process is expressed in a single number by the use of the Process Capability Index (Cpk) it gets easier for users to meet the specifications. All in all, it provides important information about the stability of the process that is expected to be uncertain with ever-changing variables.
The Process Capability Index comes in handy while solving the estimation of products in a real-life situation.
Cpk is a measurement of process capability. Process capability index measures your process to see if it is capable of making an item within the given specifications. On the other hand, the process capability index lets you know where your process is in relation to the center of those specifications. The Cp for the upper limit is represented as the Cpu, while the Cp for the lower limit is represented as the Cpl.
The Cpk equations for each are nearly identical.
The value of Cp index is not sufficient by itself to analyze a process capability. What would happen if the nominal production output value shifts towards either the upper or lower limits and some of the production falls outside the design specifications? This is when a Cpk calculation is needed
Process capability index (cpk) is the measure of process capability. It shows how closely a process is able to produce the output to its overall specifications. It decides how consistent we are to our average performance.
A person may perform with minimum variation, but he can be away from his target towards one of the specification limits that indicates the Cpk will be lower, but Cp will be high.
Cpk formula helps in calculating the process capability index (cpk), which is the measure of process capability. This value depicts how closely a process is able to produce the output to its overall specifications. Thus, deciding how consistent we are with our average performance. The development of any product or service must follow a well-structured process. The ability of this course of action will decide the successful outcome. Cpk formula helps in confirming this successful outcome of a process.
Cpk is an important statistical tool. Process capability refers to the arithmetical study of the natural process variability of the given responsibilities in consideration. Process capability index(cpk) is used for calculating the ability of the process. The cpk formula is given as,
Cpk = min[(USL−mean)/3σ, (mean−LSL)/3σ]
where,
- Cpk = Process capability index
- mean = mean value
- σ is a standard deviation
- USL is the upper specification limit
- LSL is the lower specification limit
Determine the Cpk
Once you have the Cpl and Cpu calculated, you can put this into the Cpk formula
The formula for Cpk = Min (Cpl, Cpu)
The standard deviation is multiplied by three because six standard deviations (or six sigmas), account for just about every eventuality in a process using a normal distribution curve. Six divided by two (for the upper and lower limits) is three.
How to Calculate Cp :
We use Cp & Cpk when a process is stable and Pp & Ppk when a process is new, the way you calculate each is a bit different, too.
Pp = (USL – LSL) / 6* s
In Pp, s is the standard deviation or the ‘fatness’ or dispersion of the bell curve.
In Cp, we replace s with an estimate of σ we call σr. To do that, we leverage the Moving Range concept from a Moving R Bar chart or an XMR Chart. So, σr = [ R Bar / d2]
R Bar comes from the Moving range.
D2 reflects values derived from integrating the area under the normal curve. We often use a table that gives a d2 value based on how many subgroups were in the sample.
d2 subgroup values
Cp does not account for centering.
First, Cp = (USL – LSL) / ( 6* σr )
Second, Cp = (USL – LSL) / ( 6* R Bar / d2 )
Cp for Process Mean close to USL
If your Process Mean (central tendency) is closer to the USL, use: [ USL – x(bar) ] / [3 * R Bar / d2], where x(bar) is the Process Mean.
Cp for Process Mean close to LSL
If your Process Mean (central tendency) is closer to the LSL, use: [x(bar) – LSL ] / [3 * R Bar / d2], where x(bar) is the Process Mean.
Capability Index
How do Cp, Z values, DPMO, Specification Limits, Standard Deviation, and Capability all relate?
Also, see Z values and process capability.
Capability Index
Notes on Cp Values
- If the ratio is greater than one, then the Engineering Tolerance is greater than the Process Spread, so the process has the “potential” to be capable (depending on process centering).
- If the Process Spread is greater than the Engineering Tolerance, then the process variation will not “fit” within the tolerance, and the process will not be capable (even if the process is centered appropriately).
Capability Ratio Cr
The capability ratio is the inverse of Cp
Cr = 1/ Cp = ( 6* σr ) / (USL – LSL)
If Cr < 0.75, the process is capable.
If Cr = 0.75 – 1.00, the process is capable of tight control.
When the Cr >1, the process is not capable.
Notes on Relating Cp and Cpk
- If Cp == Cpk, then the process is perfectly centered. If perfectly centered, Cp == Cpk.
- Because Cpk accounts for centering (where Cp does not), Cpk can never be larger than Cp.
- Both assume a stable process.
The Basic Concept
When the manufacturing process is being defined, your goal is to ensure that the parts produced fall within the Upper and Lower Specification Limits (USL, LSL). Process Capability measures how consistently a manufacturing process can produce parts within specifications.
The basic idea is very simple. You want your manufacturing process to:
(1) be centered over the Nominal desired by the design engineer, and
(2) with a spread narrower than the specification width.
Cp measures whether the process spread is narrower than the specification width
Cpk measures both the centering of the process as well as the spread of the process relative to the specification width
The Basic Calculations
Before we get into the detailed statistical calculations, let’s review the high-level steps:
1: Plot the Data: Record the measurement data, and plot this data on a run-chart and on a histogram as shown in the picture on the right.
2: Calculate the Spec Width: Plot the Upper Spec Limit (USL) and Lower Spec Limit (LSL) on the histogram, and calculate the Spec Width as shown below.
Spec Width = USL — LSL
3: Calculate the Process Width: Similarly, we will also calculate the Process Width. The simplest way to think about the process width is “the difference between the largest value and the smallest value this process could create”.
Process Width = UCL — LCL
4: Calculate Cp: Calculate the capability index as the ratio of the spec width to the process width.
Cp = Spec Width / Process Width
Process Stability
Before you begin a process capability analysis, you must check to ensure your process is stable. If your process is stable, the short-term behaviour of the process (during the initial run), will be a good predictor of the long-term behavior of the process (i.e. you can predict future performance with confidence).
Process behavior – both short-term and long-term – is characterized by the average and the standard deviation. A process will be considered stable when it’s average and standard deviation are constant over time.
Short-Term & Long-Term Process Behaviour
For a stable process, the run chart should look relatively flat, without an upward or downward trend, and without periodic fluctuations.
Short-Term Standard Deviation:
To calculate short-term average and standard deviation, we create sub-groups of the data. Sub-groups can be created in two ways: you can either record consecutive measurements on an individuals chart and treat every two consecutive parts as a sub-group of size 2, or you can record measurements for 3 to 5 samples at a fixed interval (e.g. 5 parts every hour) on an x-bar chart.
The average and standard deviation of these sub-group measurements are called the short-term-average and short-term-standard-deviation or within-sub-group average and standard deviation.
Long-Term Standard Deviation:
Calculating long-term average and standard deviation is much simpler. We take all the measurements from the individuals charts, or from the x-bar charts, and calculate the average and standard deviation for the entire data-set.
Difference between Cp, Cpk and Pp, Ppk
[Potential] Process Capability Analysis (Cp, Cpk):
A process capability study uses data from a sample to PREDICT the ability of a manufacturing process to produce parts conforming to specifications. This prediction enables us to “qualify” a new manufacturing process as being fit for use in production. The index Cp provides a measure of potential process capability i.e. how well a process can perform if there is no change in the underlying process conditions.
Cpk uses “s-short-term” to predict the behavior of the process.
[Actual] Process Performance Analysis (Pp, Ppk)
A process performance study is used to EVALUATE a manufacturing process and answers the question: “how did the process actually perform over a period of time?” This is a historical analysis rather than a predictive analysis, but can still be used to drive process improvements.
Ppk uses “s-long-term” to evaluate the behavior of the process.
If the process is stable, Ppk = Cpk, i.e. the actual performance will match the predicted potential performance. However, if the process is unstable &emdash; i.e. if it shifts or drifts over time &emdash; you will find Ppk << Cpk.
Difference between Cp, Cpk and Pp, Ppk
[Potential] Process Capability Analysis (Cp, Cpk):
A process capability study uses data from a sample to PREDICT the ability of a manufacturing process to produce parts conforming to specifications. This prediction enables us to “qualify” a new manufacturing process as being fit for use in production. The index Cp provides a measure of potential process capability i.e. how well a process can perform if there is no change in the underlying process conditions.
Cpk uses “s-short-term” to predict the behavior of the process.
[Actual] Process Performance Analysis (Pp, Ppk)
A process performance study is used to EVALUATE a manufacturing process and answers the question: “how did the process actually perform over a period of time?” This is a historical analysis rather than a predictive analysis, but can still be used to drive process improvements.
Ppk uses “s-long-term” to evaluate the behavior of the process.
If the process is stable, Ppk = Cpk, i.e. the actual performance will match the predicted potential performance. However, if the process is unstable & emdash; i.e. if it shifts or drifts over time &emdash; you will find Ppk << Cpk.
Uses of Cpk Formula
The process capability index or Cpk Formula is mostly used for the measurements of any achieving process. The value of Cpk is used for depicting how closely a process will be able to produce the output of its overall specifications. For calculating the performance of an average, the development of any process, product or service has to follow a well structured process. The formula of Cpk is used in confirming the successful outcome of any process.
- With the clarity on Cpk & Ppk and their formulae, check which formula your team is using to calculate Cpk.
- If you are already using short term standard deviation to calculate Cpk, then that is fine. If you are using long term standard deviation, inform your customer about the same and get it clarified.
- By correcting the formula, you will get a correct Cpk value – which your processes deserve.
- In all the reports of Cpk, try to explicitly mention whether you are using short term / long term standard deviation, preferably with formula.
- With the clarity on Cpk & Ppk and their formulae, check which formula your team is using to calculate Cpk.
- If you are already using short term standard deviation to calculate Cpk, then that is fine. If you are using long term standard deviation, inform your customer about the same and get it clarified.
- By correcting the formula, you will get a correct Cpk value – which your processes deserve.
- In all the reports of Cpk, try to explicitly mention whether you are using short term / long term standard deviation, preferably with formula.
The following can be seen from the analysis and process capability ratio:
- When Cp equals 1, the process is perfectly centered. (Cp = 1, prefect process)
- For Cp value higher than one, it means tolerance> the process. This confirms that the process appears to be able to do this. (Cp> 1, process compatible)
- If the process length is greater than the tolerance, the process variation is within the tolerance range, rendering the process incapable.
- Cpk makes it possible to measure the closeness of the performance of the process to the condition lay down by the client by allowing for the natural inconsistency of the process.
- If Cpk is a negative value, you need to make sure that the process you inherited leads to a result that is not within the range specified by the client and is completely outside.
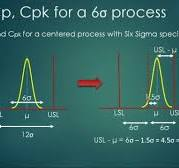
- The Cpk of 3 indicates that the output is excellent and the process has 6σ capacities and that is what we need to achieve.
- We need a Cpk of at least 1.33, which is 4σs, to satisfy most customers.
Takehome Message :
6σ is a numerical study of deviations in the process. This is important because due to such variations the result of the product or service will also vary. Usually, that is the reason the customers provide the range (lower and upper) for any product that they can accept.
In a real sense, there is no perfect process and hence no perfect product as it is very difficult to meet perfection. That is why there are certain tolerances allowed. Thus to reduce the defects in the product the process must follow some criteria so that the products fall exactly or near the center of the sigma line defined by the upper and lower tolerance levels.
As 6σ is a statistical tool that determines sigma value and the process capability ratio and process capability analysis, you might be using this very often as a process champion at your organizations.
